ESolver 模块介绍
作者:陈默涵,邮箱:mohanchen@pku.edu.cn
最后更新时间:2025 年 10 月 6 日
一、ESolver 模块介绍
1. 物理模型
- 无论是密度泛函理论计算还是分子动力学模拟,都是在给定晶格形状和大小,给定好原子坐标后计算体系的总能量。唯一较大的区别是,密度泛函理论把原子拆分成电子和离子两部分开处理,通过计算电子-电子、电子-离子、和离子-离子相互作用来获得体系总能量,而传统分子动力学方法(例如 LJ 势)一般是通过解析的势函数直接计算原子-原子间的相互作用。如果是基于机器学习的分子动力学方法,例如 DPMD 方法,则是通过神经网络来代替原子间的势函数。
- 原子算筹的 ESolver 模块(Energy Solver,简称 ESolver,代表能量求解器)的功能是在给定原子位置的前提下,通过计算该体系的总能量、得到原子的受力、原胞的应力等关键物理量。
- 在 ESolver 模块中,原子算筹提供了多种能量求解器,包括在 DFT 中通过对角化的方式求解 Kohn-Sham 方程,从而计算系统的基态电子性质。其中 Kohn-Sham 方程的求解又要区分在平面波和局域轨道两种基矢量情况下的代码。此外,ESolver 还提供诸如随机波函数密度泛函理论(Stochastic DFT)、无轨道密度泛函理论(Orbital-Free DFT)、以及随时间演化的含时密度泛函理论(rt-TDDFT)等其他电子结构的求解器。最后,ESolver 还提供了给定 LJ 势或者 DPMD 势来计算体系总能量的功能。
2. 设计思路
- ESolver 在 ABACUS 中起着非常重要的作用,属于 ABACUS 的“顶层框架设计”,从 ESolver 会分出不同的基矢量(PW 或者 LCAO),不同的能量求解方法(KSDFT、OFDFT、Stochastic DFT、real-time TDDFT 和 Linear-response TDDFT 方法等),此外还有一些经验势场,包括 DP 方法都在 ESolver 的层次实现了调用,因此有必要规范 ESolver 的写法。
二、ESolver 的设计规范
总体规范
- ESolver 里不应该包含过多程序细节,而更多展示的是代码的流程和逻辑。
- ESolver 限制数据的生命周期,但建议数据的 new 和 delete 等操作放到具体的函数里调用,另外 new 和 delete 要匹配,最大限度减小内存泄露。
- 理想的 ESolver 应该可以执行不同精度的计算,且适用于不同的超算,但不建议给 ESolver 加上新的模板参数,除非万不得已。因为模板参数往往会传染,使得代码变得臃肿。
构造函数和析构函数
- 强烈不建议在 ESolver 的构造函数和析构函数里写任何代码,容易引起难以查找的错误。
成员变量
- 我们会在每个 ESolver 里定义相关的成员变量,但需要对 DFT 算法了解比较深入。
- 例如,电荷密度既可以在 OFDFT 也可以在 KSDFT 里面被使用,而不会在 DPMD 里被使用。所以我们会把电荷密度这个物理量放在 ESolver_FP 类里进行管理,从而避免在 OFDFT 和 KSDFT 的代码里分别定义。
- 不建议使用带模板参数的成员变量,除非万不得已,已有的带模板的成员变量,后期会考虑删去一部分。
成员函数
建议开发者在 ESolver 中采用以下 11 个函数为成员函数,其它新提交的 PR 中若包含这些函数以外的成员函数,将不会被接收。
// 函数1 before_all_runners:在程序初始,离子位置开始变化之前之前需要执行的操作
ESolver::before_all_runners();
for(i=0; i<number_of_ion_steps; ++i)
{
// 函数2 runner:在离子弛豫和分子动力学的每一步调用,给定离子构型,
// 得到能量、受力、应力等信息
ESolve::runner();
// 函数3 cal_energy:计算体系总能量
ESolver::cal_energy();
// 函数4 cal_energy:计算体系原子受力
ESolver::cal_force();
// 函数5 cal_energy:计算体系应力
ESolver::cal_stress();
} // 结束离子步
// 函数6 after_all_runners:所有离子步结束之后的操作
ESolver::after_all_runners();
在 runner()函数内部有以下一些成员函数。如果以下函数不满足需求,可以重载 runner 函数
ESolver::runner()
{
//函数7 before_scf: 电子自洽迭代循环之前做的操作,包括检查离子位置变化
// 带来的一些物理量的更新
ESolver::before_scf();
// 电子迭代循环
for(iter=0; iter<number_of_scf_iterations; ++iter)
{
// 函数8 iter_init:在每次电子scf迭代之前的准备工作
ESolver::iter_init();
// 函数9 hamilt2density:构造哈密顿量,并且从哈密顿量解出电子密度
ESolver::hamilt2density();
// 函数10 iter_finish:每步电子步迭代之后的操作
ESolver::iter_finish();
}// end iter
// 函数11 after_scf:如果电子迭代结束(收敛或达到最大允许步数),
// 需要做的操作
ESolver::after_scf()
}// end runner
三、代码介绍
1. 代码位置
- ESolver 代码的位置在/source/module_esolver/
- 整个模块的名字空间(namespace)为 ModuleESolver
2. 代码框架图
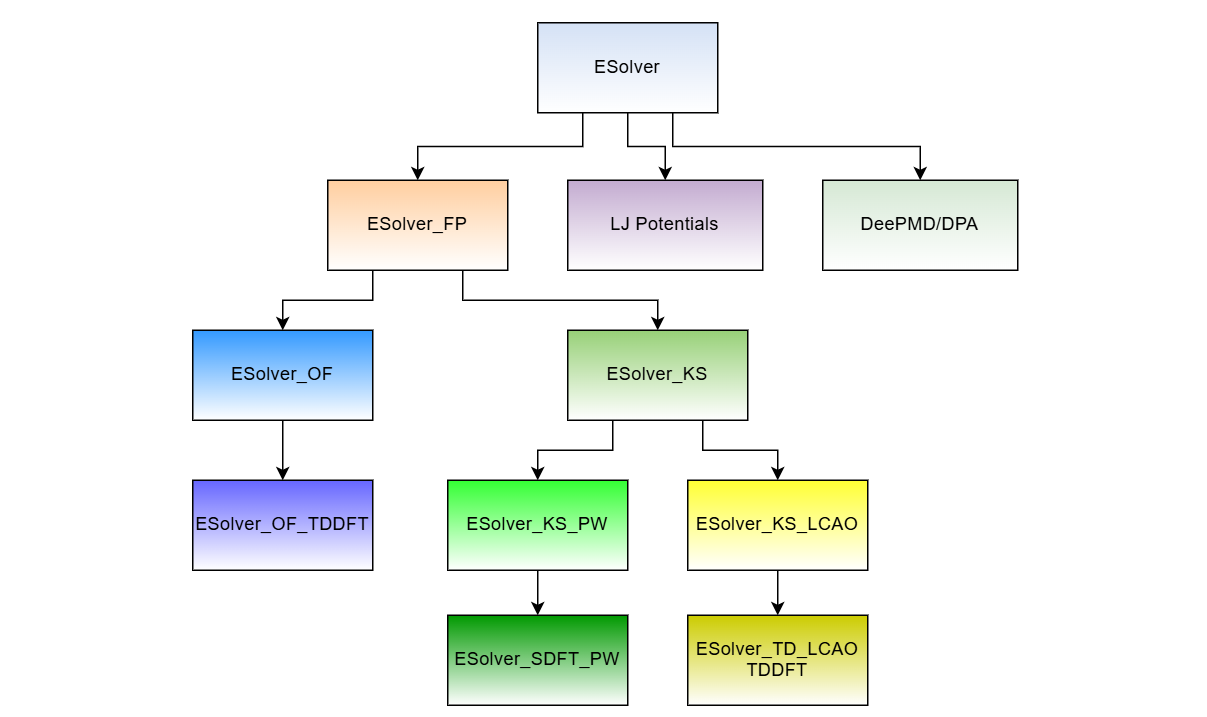
图:能量求解器 ESolver 的框架图。ESolver 分成两大部分:第一性原理的能量求解器 ESolver_FP 和经验势的求解器。其中 ESolver_FP 又派生出无轨道密度泛函理论求解器 ESolver_OF(用平面波基矢量)和 Kohn-Sham 密度泛函理论求解器 ESolver_KS。其中 ESolver_KS 需要波函数 Psi,电子信息 ElecState,和电子哈密顿量求解器 HSolver 作为输入,同时可以派生出不同基矢量的能量求解器。
3. 模块关系图
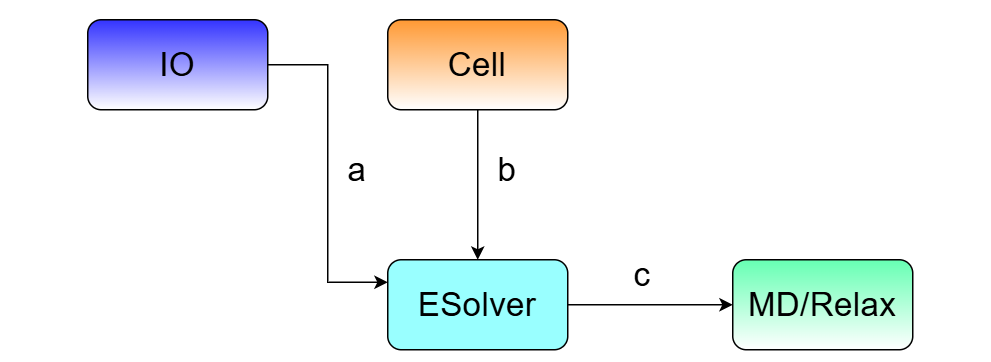
图:a. IO 模块提供 ESolver 需要的输入参数和物理量输出接口; b. Cell 模块作为 ESolver 模块的核心输入,是 ESolver 的求解目标,ESolver 中的 Cell 模块对象是只读的; c. ESolver 提供 MD 和 Relax 模块需要的系统势能和原子受力、应力等信息;
四、主要功能
每个功能里可以加关键算法和参考文献。
esolver.h
基类,其子类只能使用其定义的虚函数接口。
esolver_fp.h
第一性原理方法类,继承了 esolver.h 定义的类,其成员包含电荷密度,结构因子,电荷密度外插,溶剂模型等,可用于派生 OFDFT 或者 KSDFT 类。
esolver_ks.h
继承了 esolver_fp.h 的类,适用于求解 Kohn-Sham 方程,但不限于基组。其成员包含波函数,电荷密度混合,非局域赝势等。可用于派生不同基组的类。
esolver_ks_pw
继承了 esolver_ks.h 的类,采用平面波基组求解 KS 方程。其成员包含平面波波函数等。可用于派生例如 SDFT 类。
esolver_ks_lcao
继承了 esolver_ks.h 的类,采用数值原子轨道基组求解 KS 方程。其成员包含寻找近邻点,格点积分,原子轨道并行分配,双中心积分,轨道信息等。可用于派生基于数值原子轨道的 rt-TDDFT 等类。
esolver_ks_lcao_tddft
继承了 esolver_ks_lcao.h 的类,支持采用数值原子轨道进行 real-time TDDFT 计算。
esolver_sdft_pw
继承了 esolver_ks_pw.h 的类,支持采用平面波进行 stochastic DFT 的计算。采用切比雪夫展开和随机波函数的方法进行电子密度的计算,之后还是采用自洽迭代的方法求出体系的基态电子密度。
esolver_of
继承了 esolver_fp.h 的类,支持采用平面波进行 OFDFT 的计算。
esolver_of_tddft
继承了 esolver_of.h 的类,,支持采用平面波进行 real time OFDFT 的计算。
esolver_dp
继承了 esolver.h 的类。基于机器学习的分子动力学 DPMD 方法。如果预处理定义了__DPMD,则可以支持 ABACUS+DPMD 的计算。
esolver_lj
继承了 esolver.h 的类。支持 LJ 经验势的计算。
五、ESolver 重构计划
- 规范成员变量和成员函数所属层级以及访问权限,关于 ESolver 允许的成员变量的规范仍在制定之中,之后会重新设计成员变量。
- ESolver 是否采用模板,以及哪些是模板参数,需要重新评估。
- 将 ESolver 的继承关系转化为组合的形式,删除没必要的继承。
- 根据新功能添加更多的 ESolver,例如基于 LCAO 轨道的 DFPT 方法,基于 PW 的 DFPT 方法等等。